15. 散布図・バブルチャート#

15.1. 概要#

散布図（Scatter） とは，主に二つの量的変数に対して，一つ一つのデータを ドットの位置 で表すグラフです．ドットの色で三つ目の変数を表現することもあります．

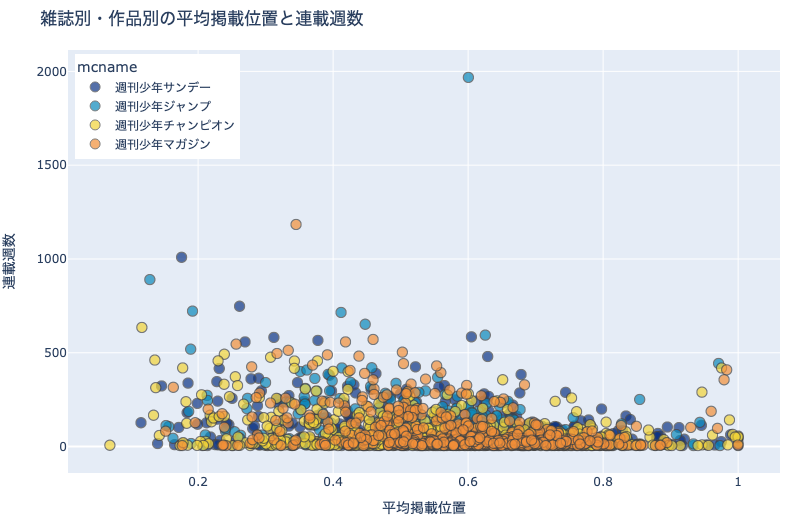
例えば上図は，作品の

平均掲載位置（横方向の位置）
掲載週数（縦方向の位置）
雑誌（ドットの色）

を表した散布図です．

バブルチャート（Bubble Chart) とは，散布図を拡張し， ドットの大きさ を利用することで三つ目の量的変数を表現するグラフです．ただし，「ドットの大きさ」に関しては，（全体的な傾向は掴めるものの）個別の比較は難しいことにご注意ください．

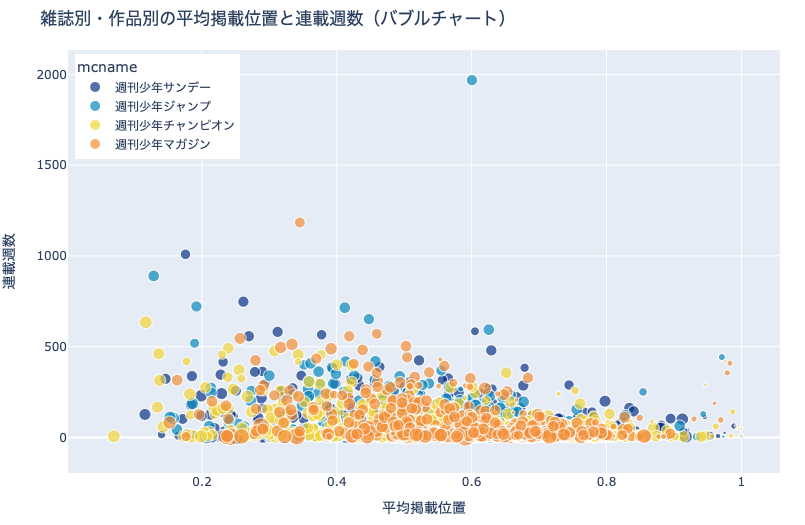
例えば上図は，作品の

平均掲載位置（横方向の位置）
連載週数（縦方向の位置）
雑誌（ドットの色）
平均ページ数（ドットの大きさ）

を表したバブルチャートです．平均掲載位置や連載週数の比較は容易ですが，個別の作品の平均ページ数を比較するのは非常に難しいことがわかります．この課題は，散布図行列を採用することで回避できます．

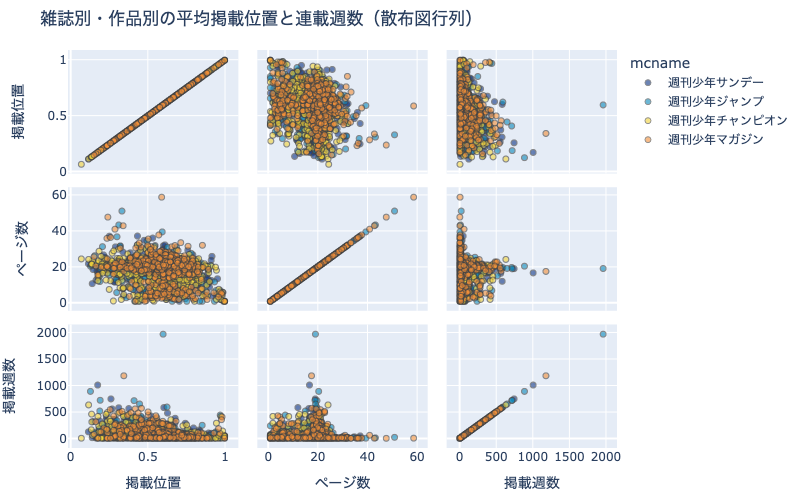
散布図行列（Scatter Matrix) とは，複数の量的変数に対して，全ての組合せの散布図を行列上に配置するグラフです．対角成分をヒストグラムや密度プロットにする実装もあります．一つ一つの図が小さくなってしまいますが，三つ以上の量的変数の関係を把握する際に便利です．

15.2. Plotlyによる作図方法#

Plotlyにおいては，plotly.express.scatter()を用いて散布図やバブルチャートを作図できます．

import plotly.express as px
fig = px.scatter(
    df, x='col_x', y='col_y')

上記の例では，dfのcol_x列を横軸，col_y列を縦軸に取った散布図のオブジェクトfigを作成します．更に，三つ目の変数に相当する列をsizeで指定することで，

fig = px.scatter(
    df, x='col_x', y='col_y', size='col_size')

バブルチャートのオブジェクトfigを作成できます．

散布図行列を作図する場合は，plotly.express.scatter_matrix()を利用します．

fig = px.scatter_matrix(
    df, dimensions=['col_0', 'col_1', 'col_2'])

上記の例では，dfのcol_0・col_1・col_2列を対象とした散布図行列のオブジェクトfigを作成します．もちろん，dimensionsで指定することで，三つ以上の変数を対象とすることも可能です．

15.3. MADB Labを用いた作図例#

15.3.1. 下準備#

import pandas as pd
import plotly.express as px

import warnings
warnings.filterwarnings('ignore')

# 前処理の結果，以下に分析対象ファイルが格納されていることを想定
PATH_DATA = '../../data/preprocess/out/episodes.csv'
# Jupyter Book用のPlotlyのrenderer
RENDERER = 'plotly_mimetype+notebook'

# 連載週数の最小値
MIN_WEEKS = 5

def show_fig(fig, adjust_legend=True):
    """Jupyter Bookでも表示可能なようRendererを指定"""
    fig.update_layout(margin=dict(t=50, l=25, r=25, b=25))
    if adjust_legend:
        fig.update_layout(legend={
            'yanchor': 'top',
            'xanchor': 'left',
            'x': 0.01, 'y': 0.99})
    fig.show(renderer=RENDERER)

df = pd.read_csv(PATH_DATA)

15.3.2. 作品別の平均掲載位置と連載週数#

df_plot = \
    df.groupby('cname')['pageStartPosition'].\
    agg(['count', 'mean']).reset_index()
df_plot.columns = ['cname', 'weeks', 'position']
df_plot = \
    df_plot[df_plot['weeks'] >= MIN_WEEKS].reset_index(drop=True)

fig = px.scatter(
    df_plot, x='position', y='weeks', opacity=0.7, 
    hover_data=['cname'], title='作品別の平均掲載位置と連載週数')
fig.update_traces(
    marker={'size': 10, 'line_width':1,})
fig.update_xaxes(title='平均掲載位置')
fig.update_yaxes(title='連載週数')
show_fig(fig)

15.3.3. 雑誌別・作品別の平均掲載位置と連載週数#

df_plot = \
    df.groupby(['mcname', 'cname'])['pageStartPosition'].\
    agg(['count', 'mean']).reset_index()
df_plot.columns = ['mcname', 'cname', 'weeks', 'position']
df_plot = \
    df_plot[df_plot['weeks'] >= MIN_WEEKS].reset_index(drop=True)

fig = px.scatter(
    df_plot, x='position', y='weeks', color='mcname', 
    opacity=0.7,
    hover_data=['cname'], 
    color_discrete_sequence= px.colors.diverging.Portland,
    title='雑誌別・作品別の平均掲載位置と連載週数')
fig.update_traces(
    marker={'size': 10, 'line_width':1})
fig.update_xaxes(title='平均掲載位置')
fig.update_yaxes(title='連載週数')
show_fig(fig)

15.3.4. 雑誌別・作品別の平均掲載位置と連載週数と平均ページ数（バブルチャート）#

df_plot = \
    df.groupby(['mcname', 'cname'])\
    [['pages', 'pageStartPosition']].\
    agg(['count', 'mean']).reset_index()
df_plot.columns = [
    'mcname', 'cname', 'weeks', 'pages',
    '_weeks', 'position']
df_plot = \
    df_plot[df_plot['weeks'] >= MIN_WEEKS].reset_index(drop=True)

fig = px.scatter(
    df_plot, x='position', y='weeks', color='mcname',
    size='pages', opacity=0.7,
    color_discrete_sequence= px.colors.diverging.Portland,
    hover_data=['cname'], 
    title='雑誌別・作品別の平均掲載位置と連載週数（バブルチャート）')
fig.update_traces(
    marker={'line_width':1})
fig.update_xaxes(title='平均掲載位置')
fig.update_yaxes(title='連載週数')

show_fig(fig)

15.3.5. 雑誌別・作品別の平均掲載位置と連載週数と平均ページ数（散布図行列）#

df_plot = \
    df.groupby(['mcname', 'cname'])\
    [['pages', 'pageStartPosition']].\
    agg(['count', 'mean']).reset_index()
df_plot.columns = [
    'mcname', 'cname', 'weeks', 'pages',
    '_weeks', 'position']
df_plot = df_plot[[
    'mcname', 'position', 'pages', 'weeks']]
df_plot = \
    df_plot[df_plot['weeks'] >= MIN_WEEKS].reset_index(drop=True)

fig = px.scatter_matrix(
    df_plot, dimensions=['position', 'pages', 'weeks'], 
    color='mcname', opacity=0.6, height=500,
    color_discrete_sequence= px.colors.diverging.Portland,
    labels={
        'position': '掲載位置', 'weeks': '掲載週数',
        'pages': 'ページ数'},
    title='雑誌別・作品別の平均掲載位置と連載週数（散布図行列）')
fig.update_traces(marker={'line_width':1})
show_fig(fig, adjust_legend=False)

バブルチャートではおぼろげにしかわからなかった

平均ページ数の分布
平均ページ数と他の変数との関係

がよくわかるようになりました．一つ一つの散布図が小さくなってしまうという欠点がありますが，個人的には，バブルチャートより散布図行列を使うことが多いです．

マンガと学ぶデータビジュアライゼーション

散布図・バブルチャート

Contents